Efficient blocked Gibbs sampler for a Bayesian linear regression model with random intercepts. The fixed effects (regression coefficients) and the random effects (intercepts) are sampled *jointly* for Monte Carlo efficiency, while the variance components are sampled in a separate block. The model uses a horseshoe prior for the fixed effects (regression coefficients).
Arguments
- Y
(
m x n) matrix of response variables- X
(
n x p) matrix of covariates- nsave
number of MCMC iterations to record
- nburn
number of MCMC iterations to discard (burn-in)
Value
a list containing the following elements:
coefficientsthe estimated regression coefficients (posterior means)fitted.valuesthe fitted values (posterior means)post_y_predposterior predictive drawspost_y_pred_sumposterior predictive totals for each subjectpost_betaposterior draws of the regression coefficientspost_uposterior draws of the random interceptspost_sigma_uposterior draws of the random intercept standard deviationpost_sigma_eposterior draws of the observation error standard deviationpost_lpdposterior draws of the log-likelihood (i.e., the log-likelihood evaluated at each posterior draw of the model parameters)
Examples
# Simulate some data:
dat = simulate_lm_randint(n = 100, # subjects
p = 15, # covariates
m = 4) # replicates per subject
Y = dat$Y; X = dat$X
# Dimensions:
dim(Y) # m x n
#> [1] 4 100
dim(X) # n x p
#> [1] 100 16
# Fit the model:
fit = bayeslmm(Y = Y, X = X) # should take a few seconds
names(fit) # what is returned
#> [1] "coefficients" "fitted.values" "post_y_pred" "post_y_pred_sum"
#> [5] "post_beta" "post_u" "post_sigma_u" "post_sigma_e"
#> [9] "post_lpd"
# Estimated coefficients:
coef(fit)
#> [1] -1.08437785 0.91612472 0.71096223 1.11413442 -0.96520313 -0.71690658
#> [7] -0.03455753 -0.17170883 0.16787932 -0.01069944 0.02424872 -0.07709557
#> [13] -0.02726036 0.19529222 0.02857697 -0.02114447
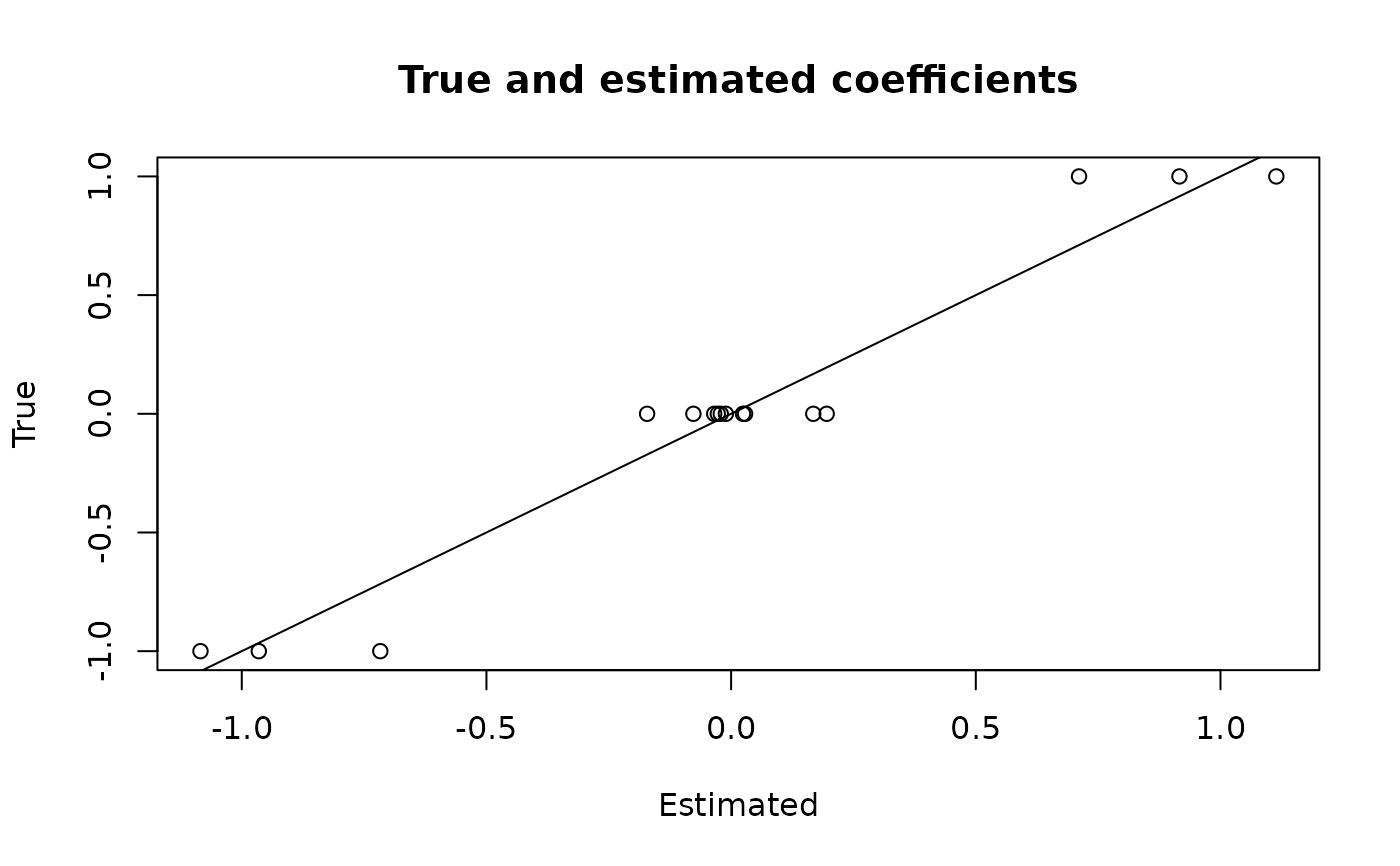
# Compare to ground truth:
plot(coef(fit), dat$beta_true,
main = 'True and estimated coefficients',
xlab = 'Estimated', ylab = 'True')
abline(0,1)
 # 90% credible intervals:
ci_beta = t(apply(fit$post_beta, 2,
quantile, c(0.05, 0.95)))
# Fitted values (m x n):
dim(fitted(fit))
#> [1] 4 100
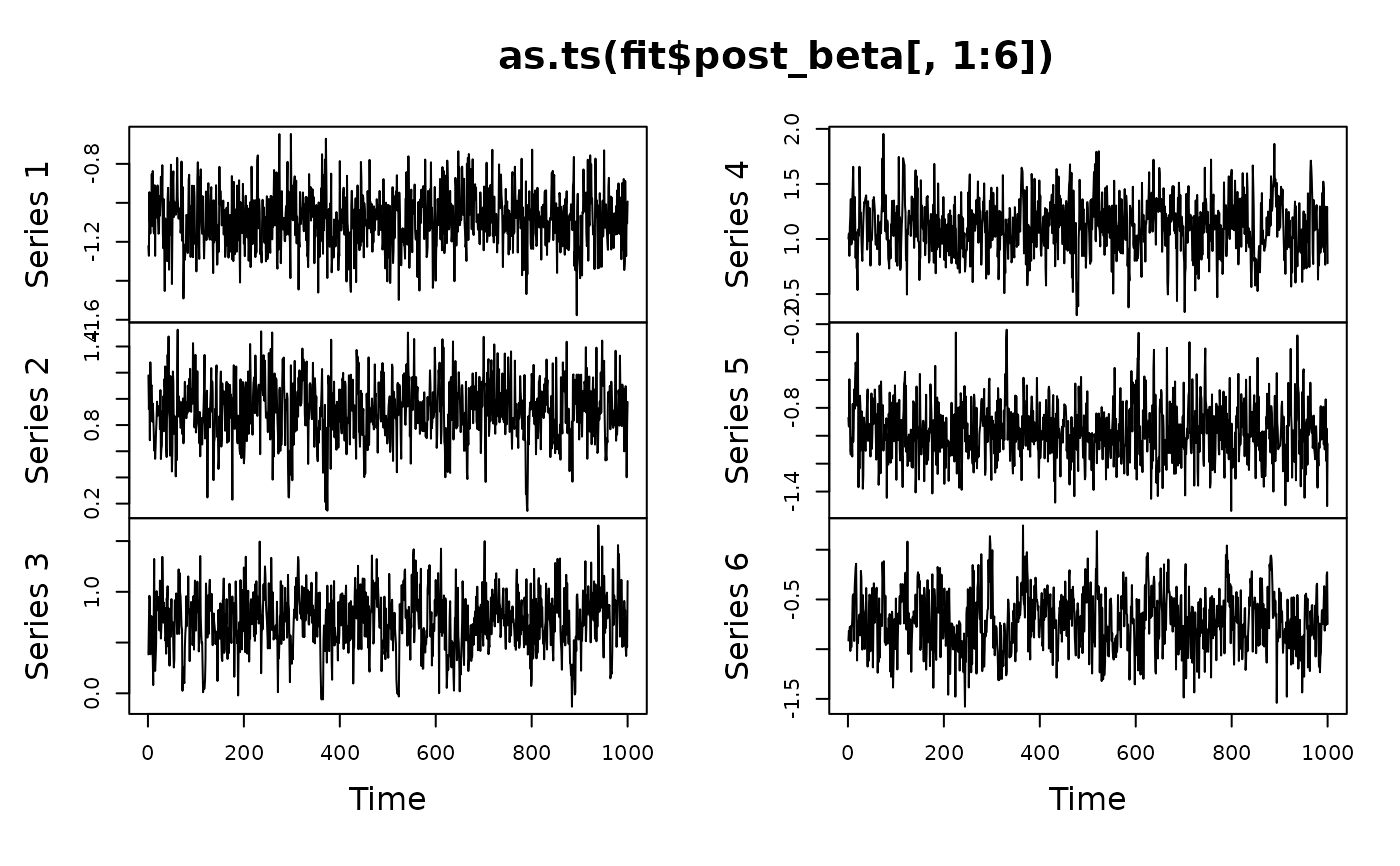
# MCMC diagnostics:
plot(as.ts(fit$post_beta[,1:6]))
# 90% credible intervals:
ci_beta = t(apply(fit$post_beta, 2,
quantile, c(0.05, 0.95)))
# Fitted values (m x n):
dim(fitted(fit))
#> [1] 4 100
# MCMC diagnostics:
plot(as.ts(fit$post_beta[,1:6]))