Skip to contents

Get posterior predictive draws and log-predictive density

Source: R/helpers.R
post_predict.Rd

Given posterior samples from the conditional mean and conditional standard deviation of a Gaussian regression model, compute posterior predictive draws and the log-predictive density (lpd) at the observed data points (draw-by-draw).

Usage

post_predict(post_y_hat, post_sigma, yy = NULL)

Arguments

post_y_hat

nsave x n draws of the conditional mean

post_sigma

nsave draws of the conditional standard deviation

yy

optional n-dimensional vector of data points; if NULL, the lpd is not computed

Value

a list with the following elements:

  • post_y_pred: nsave x n posterior predictive draws

  • post_lpd: nsave x n evaluations of the log-predictive density

Examples

# Simulate data:
dat = simulate_lm(n = 100, p = 10)
y = dat$y; X = dat$X

# Fit a Bayesian linear model:
fit = bayeslm::bayeslm(y ~ X[,-1], # intercept already included
              N = 1000, burnin = 500) # small sim for ex
#> horseshoe prior 
#> fixed running time 0.00186602
#> sampling time 0.0284795

# Compute predictive draws:
temp = post_predict(post_y_hat = tcrossprod(fit$beta, X),
                    post_sigma = fit$sigma,
                    yy = y)
names(temp) # what is returned
#> [1] "post_y_pred" "post_lpd"   

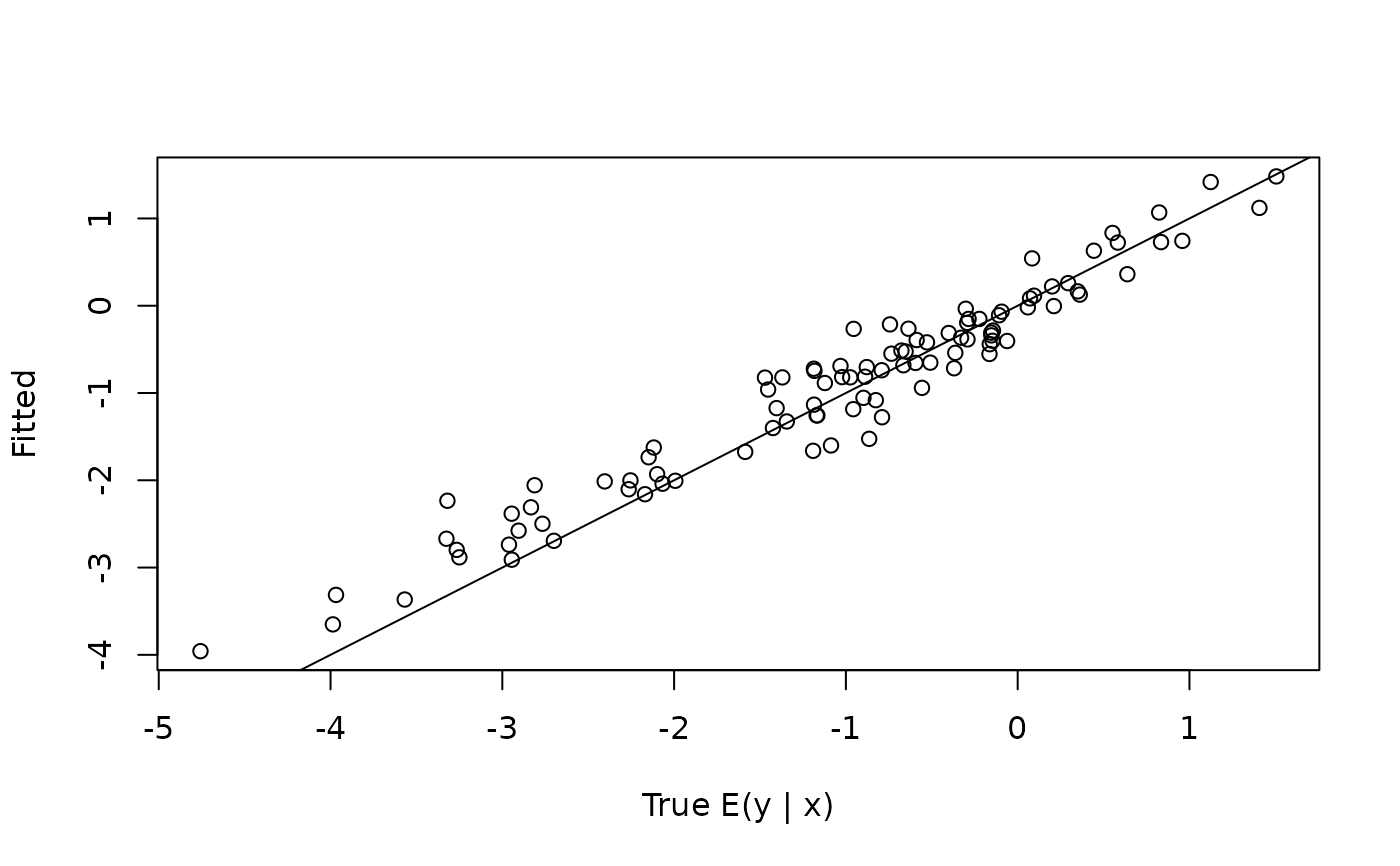
# Compare fitted values to the truth:
plot(dat$Ey_true,
     colMeans(temp$post_y_pred),
     xlab = 'True E(y | x)', ylab = 'Fitted')
abline(0,1)