Skip to contents

Bayesian spline model with a Box-Cox transformation

Source: R/source_compete.R
bsm_bc.Rd

MCMC sampling for Bayesian spline regression with a (known or unknown) Box-Cox transformation.

Usage

bsm_bc(
  y,
  x = NULL,
  x_test = NULL,
  psi = NULL,
  lambda = NULL,
  sample_lambda = TRUE,
  nsave = 1000,
  nburn = 1000,
  nskip = 0,
  verbose = TRUE
)

Arguments

y

n x 1 vector of observed counts

x

n x 1 vector of observation points; if NULL, assume equally-spaced on [0,1]

x_test

n_test x 1 vector of testing points; if NULL, assume equal to x

psi

prior variance (inverse smoothing parameter); if NULL, sample this parameter

lambda

Box-Cox transformation; if NULL, estimate this parameter

sample_lambda

logical; if TRUE, sample lambda, otherwise use the fixed value of lambda above or the MLE (if lambda unspecified)

nsave

number of MCMC iterations to save

nburn

number of MCMC iterations to discard

nskip

number of MCMC iterations to skip between saving iterations, i.e., save every (nskip + 1)th draw

verbose

logical; if TRUE, print time remaining

Value

a list with the following elements:

  • coefficients the posterior mean of the regression coefficients

  • fitted.values the posterior predictive mean at the test points x_test

  • post_theta: nsave x p samples from the posterior distribution of the regression coefficients

  • post_ypred: nsave x n_test samples from the posterior predictive distribution at x_test

  • post_g: nsave posterior samples of the transformation evaluated at the unique y values

  • post_lambda nsave posterior samples of lambda

  • model: the model fit (here, sbsm_bc)

as well as the arguments passed in.

Details

This function provides fully Bayesian inference for a transformed spline model via MCMC sampling. The transformation is parametric from the Box-Cox family, which has one parameter lambda. That parameter may be fixed in advanced or learned from the data.

Note

Box-Cox transformations may be useful in some cases, but in general we recommend the nonparametric transformation (with Monte Carlo, not MCMC sampling) in sbsm.

Examples

# Simulate some data:
n = 100 # sample size
x = sort(runif(n)) # observation points

# Transform a noisy, periodic function:
y = g_inv_bc(
  sin(2*pi*x) + sin(4*pi*x) + rnorm(n, sd = .5),
             lambda = .5) # Signed square-root transformation

# Fit the Bayesian spline model with a Box-Cox transformation:
fit = bsm_bc(y = y, x = x)
#> [1] "0 seconds remaining"
#> [1] "Total time:  0 seconds"
names(fit) # what is returned
#>  [1] "coefficients"  "fitted.values" "post_theta"    "post_ypred"   
#>  [5] "post_g"        "post_lambda"   "model"         "y"            
#>  [9] "X"             "psi"          
round(quantile(fit$post_lambda), 3) # summary of unknown Box-Cox parameter
#>    0%   25%   50%   75%  100% 
#> 0.486 0.620 0.656 0.695 0.856 

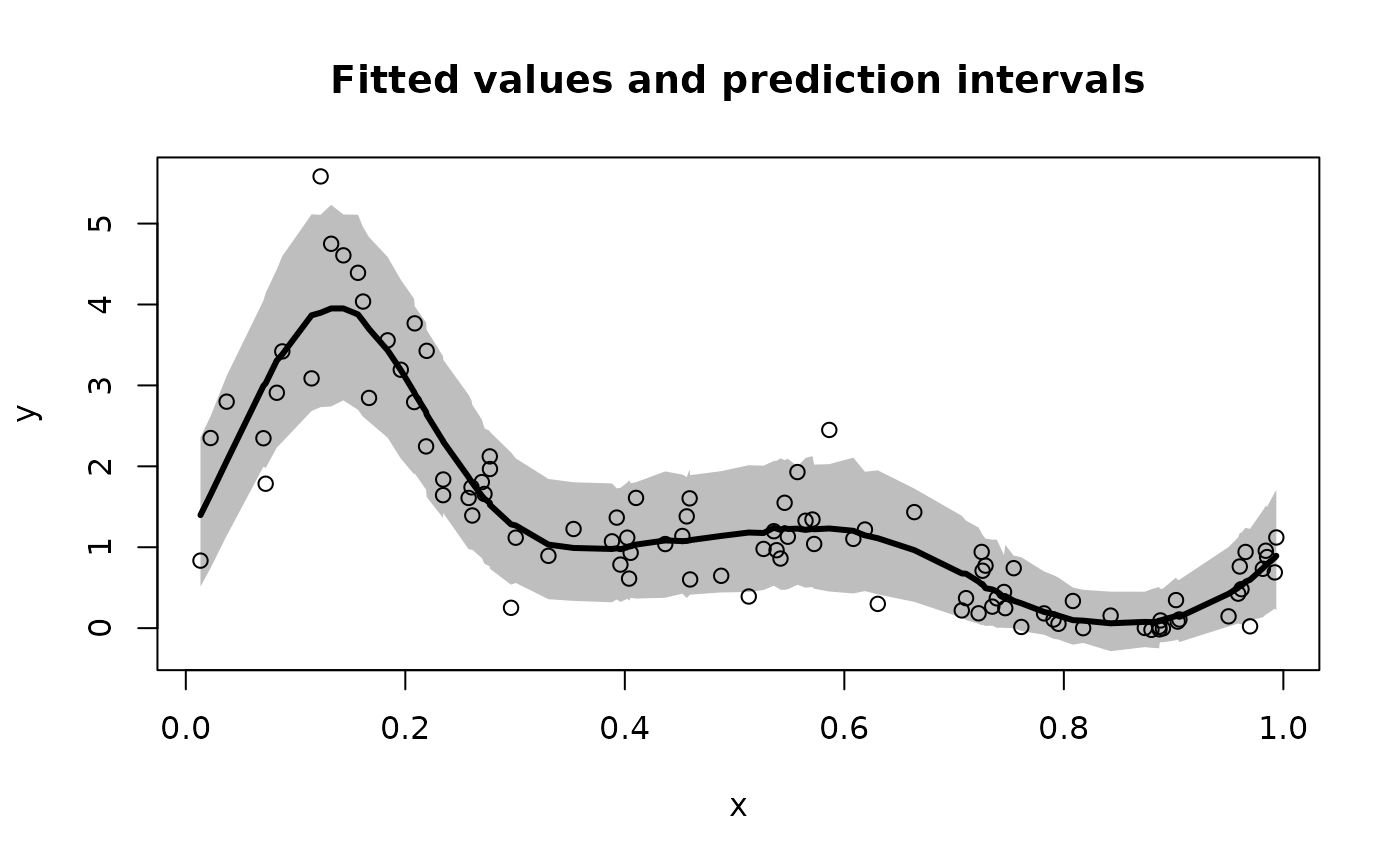
# Plot the model predictions (point and interval estimates):
pi_y = t(apply(fit$post_ypred, 2, quantile, c(0.05, .95))) # 90% PI
plot(x, y, type='n', ylim = range(pi_y,y),
     xlab = 'x', ylab = 'y', main = paste('Fitted values and prediction intervals'))
polygon(c(x, rev(x)),c(pi_y[,2], rev(pi_y[,1])),col='gray', border=NA)
lines(x, y, type='p')
lines(x, fitted(fit), lwd = 3)