Skip to contents

Semiparametric Bayesian quantile regression

Source: R/source_sba.R
sbqr.Rd

MCMC sampling for Bayesian quantile regression with an unknown (nonparametric) transformation. Like in traditional Bayesian quantile regression, an asymmetric Laplace distribution is assumed for the errors, so the regression models targets the specified quantile. However, these models are often woefully inadequate for describing observed data. We introduce a nonparametric transformation to improve model adequacy while still providing inference for the regression coefficients and the specified quantile. A g-prior is assumed for the regression coefficients.

Usage

sbqr(
  y,
  X,
  tau = 0.5,
  X_test = X,
  psi = length(y),
  laplace_approx = TRUE,
  fixedX = TRUE,
  approx_g = FALSE,
  nsave = 1000,
  nburn = 100,
  ngrid = 100,
  verbose = TRUE
)

Arguments

y

n x 1 response vector

X

n x p matrix of predictors (no intercept)

tau

the target quantile (between zero and one)

X_test

n_test x p matrix of predictors for test data; default is the observed covariates X

psi

prior variance (g-prior)

laplace_approx

logical; if TRUE, use a normal approximation to the posterior in the definition of the transformation; otherwise the prior is used

fixedX

logical; if TRUE, treat the design as fixed (non-random) when sampling the transformation; otherwise treat covariates as random with an unknown distribution

approx_g

logical; if TRUE, apply large-sample approximation for the transformation

nsave

number of MCMC iterations to save

nburn

number of MCMC iterations to discard

ngrid

number of grid points for inverse approximations

verbose

logical; if TRUE, print time remaining

Value

a list with the following elements:

  • coefficients the posterior mean of the regression coefficients

  • fitted.values the estimated tauth quantile at test points X_test

  • post_theta: nsave x p samples from the posterior distribution of the regression coefficients

  • post_ypred: nsave x n_test samples from the posterior predictive distribution at test points X_test

  • post_qtau: nsave x n_test samples of the tauth conditional quantile at test points X_test

  • post_g: nsave posterior samples of the transformation evaluated at the unique y values

  • model: the model fit (here, sbqr)

as well as the arguments passed in.

Details

This function provides fully Bayesian inference for a transformed quantile linear model. The transformation is modeled as unknown and learned jointly with the regression coefficients (unless approx_g = TRUE, which then uses a point approximation). This model applies for real-valued data, positive data, and compactly-supported data (the support is automatically deduced from the observed y values). The results are typically unchanged whether laplace_approx is TRUE/FALSE; setting it to TRUE may reduce sensitivity to the prior, while setting it to FALSE may speed up computations for very large datasets. Similarly, treating the covariates as fixed (fixedX = TRUE) can substantially improve computing efficiency, so we make this the default.

Note

The location (intercept) is not identified, so any intercepts in X and X_test will be removed. The model-fitting *does* include an internal location-scale adjustment, but the function only outputs inferential summaries for the identifiable parameters.

Examples

# \donttest{
# Simulate some heteroskedastic data (no transformation):
dat = simulate_tlm(n = 200, p = 10, g_type = 'box-cox', heterosked = TRUE, lambda = 1)
y = dat$y; X = dat$X # training data
y_test = dat$y_test; X_test = dat$X_test # testing data

# Target this quantile:
tau = 0.05

# Fit the semiparametric Bayesian quantile regression model:
fit = sbqr(y = y, X = X, tau = tau, X_test = X_test)
#> [1] "3 sec remaining"
#> [1] "2 sec remaining"
#> [1] "0 sec remaining"
#> [1] "Total time: 6 seconds"
names(fit) # what is returned
#>  [1] "coefficients"   "fitted.values"  "post_theta"     "post_ypred"    
#>  [5] "post_qtau"      "post_g"         "model"          "y"             
#>  [9] "X"              "X_test"         "psi"            "laplace_approx"
#> [13] "fixedX"         "approx_g"       "tau"           

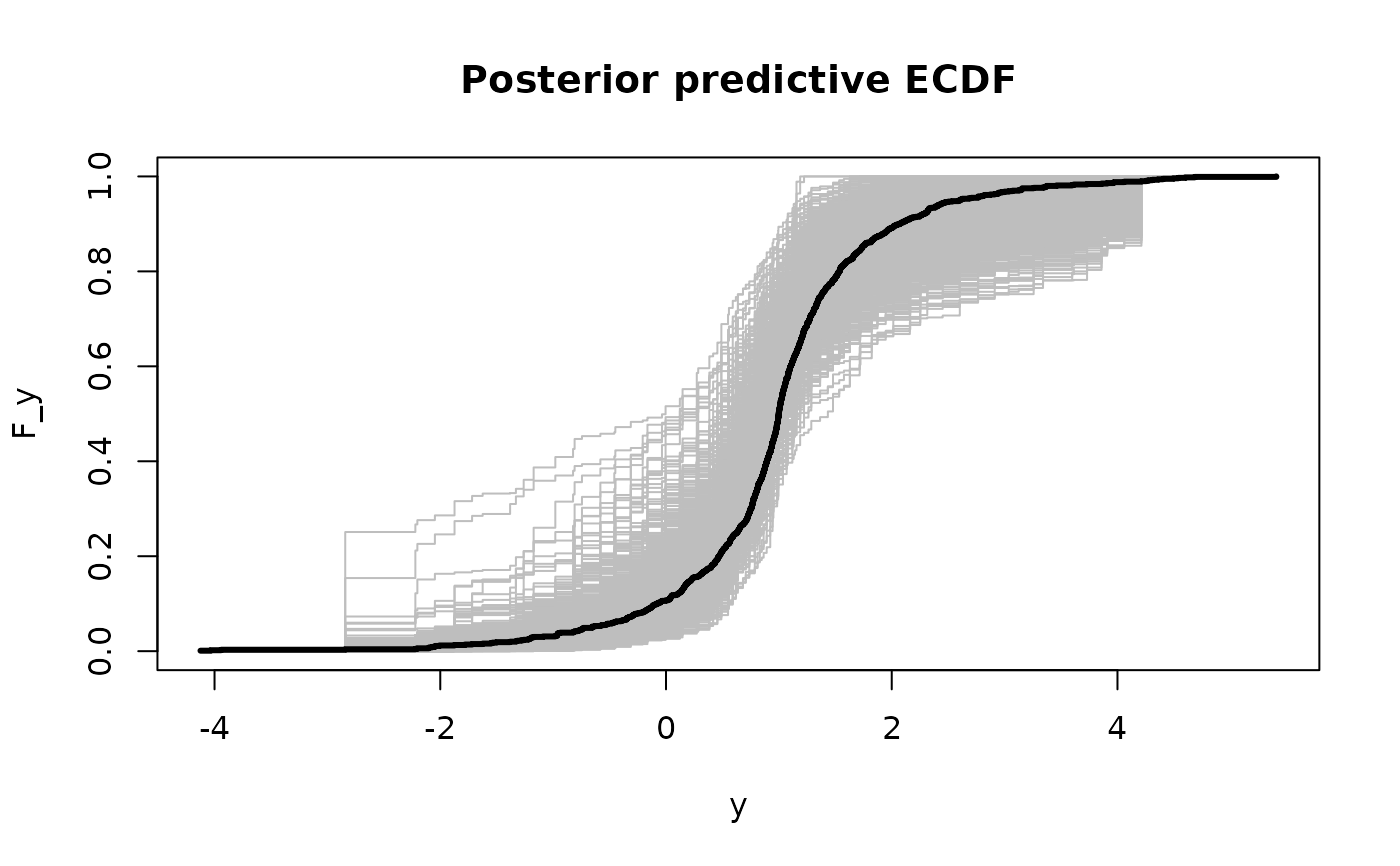
# Posterior predictive checks on testing data: empirical CDF
y0 = sort(unique(y_test))
plot(y0, y0, type='n', ylim = c(0,1),
     xlab='y', ylab='F_y', main = 'Posterior predictive ECDF')
temp = sapply(1:nrow(fit$post_ypred), function(s)
  lines(y0, ecdf(fit$post_ypred[s,])(y0), # ECDF of posterior predictive draws
        col='gray', type ='s'))
lines(y0, ecdf(y_test)(y0),  # ECDF of testing data
     col='black', type = 's', lwd = 3)

# }