Skip to contents

Bayesian Gaussian processes with a Box-Cox transformation

Source: R/source_compete.R
bgp_bc.Rd

MCMC sampling for Bayesian Gaussian process regression with a (known or unknown) Box-Cox transformation.

Usage

bgp_bc(
  y,
  locs,
  X = NULL,
  covfun_name = "matern_isotropic",
  locs_test = locs,
  X_test = NULL,
  nn = 30,
  emp_bayes = TRUE,
  lambda = NULL,
  sample_lambda = TRUE,
  nsave = 1000,
  nburn = 1000,
  nskip = 0
)

Arguments

y

n x 1 response vector

locs

n x d matrix of locations

X

n x p design matrix; if unspecified, use intercept only

covfun_name

string name of a covariance function; see ?GpGp

locs_test

n_test x d matrix of locations at which predictions are needed; default is locs

X_test

n_test x p design matrix for test data; default is X

nn

number of nearest neighbors to use; default is 30 (larger values improve the approximation but increase computing cost)

emp_bayes

logical; if TRUE, use a (faster!) empirical Bayes approach for estimating the mean function

lambda

Box-Cox transformation; if NULL, estimate this parameter

sample_lambda

logical; if TRUE, sample lambda, otherwise use the fixed value of lambda above or the MLE (if lambda unspecified)

nsave

number of MCMC iterations to save

nburn

number of MCMC iterations to discard

nskip

number of MCMC iterations to skip between saving iterations, i.e., save every (nskip + 1)th draw

Value

a list with the following elements:

  • coefficients the posterior mean of the regression coefficients

  • fitted.values the posterior predictive mean at the test points locs_test

  • fit_gp the fitted GpGp_fit object, which includes covariance parameter estimates and other model information

  • post_ypred: nsave x n_test samples from the posterior predictive distribution at locs_test

  • post_g: nsave posterior samples of the transformation evaluated at the unique y values

  • post_lambda nsave posterior samples of lambda

  • model: the model fit (here, bgp_bc)

as well as the arguments passed in.

Details

This function provides Bayesian inference for transformed Gaussian processes. The transformation is parametric from the Box-Cox family, which has one parameter lambda. That parameter may be fixed in advanced or learned from the data. For computational efficiency, the Gaussian process parameters are fixed at point estimates, and the latent Gaussian process is only sampled when emp_bayes = FALSE.

Note

Box-Cox transformations may be useful in some cases, but in general we recommend the nonparametric transformation (with Monte Carlo, not MCMC sampling) in sbgp.

Examples

# \donttest{
# Simulate some data:
n = 200 # sample size
x = seq(0, 1, length = n) # observation points

# Transform a noisy, periodic function:
y = g_inv_bc(
  sin(2*pi*x) + sin(4*pi*x) + rnorm(n, sd = .5),
             lambda = .5) # Signed square-root transformation

# Package we use for fast computing w/ Gaussian processes:
library(GpGp)

# Fit a Bayesian Gaussian process with Box-Cox transformation:
fit = bgp_bc(y = y, locs = x)
#> [1] "Initial GP fit..."
#> [1] "Updated GP fit..."
names(fit) # what is returned
#> [1] "coefficients"  "fitted.values" "fit_gp"        "post_ypred"   
#> [5] "post_g"        "post_lambda"   "model"         "y"            
#> [9] "X"            
coef(fit) # estimated regression coefficients (here, just an intercept)
#> [1] 0.2221117
class(fit$fit_gp) # the GpGp object is also returned
#> [1] "GpGp_fit"
round(quantile(fit$post_lambda), 3) # summary of unknown Box-Cox parameter
#>    0%   25%   50%   75%  100% 
#> 0.681 0.779 0.805 0.832 0.922 

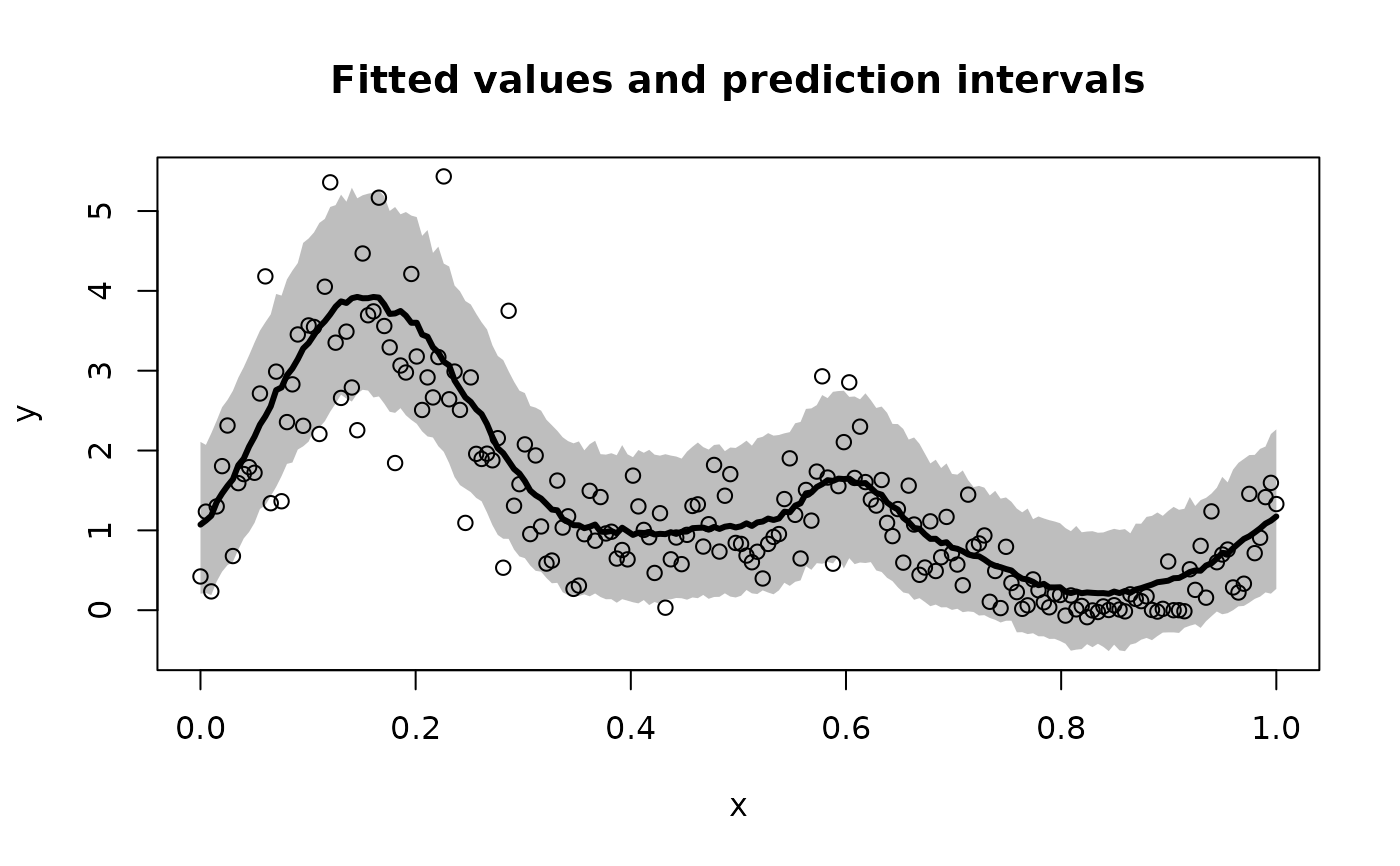
# Plot the model predictions (point and interval estimates):
pi_y = t(apply(fit$post_ypred, 2, quantile, c(0.05, .95))) # 90% PI
plot(x, y, type='n', ylim = range(pi_y,y),
     xlab = 'x', ylab = 'y', main = paste('Fitted values and prediction intervals'))
polygon(c(x, rev(x)),c(pi_y[,2], rev(pi_y[,1])),col='gray', border=NA)
lines(x, y, type='p')
lines(x, fitted(fit), lwd = 3)

# }