Skip to contents

Bayesian quantile regression

Source: R/source_compete.R
bqr.Rd

MCMC sampling for Bayesian quantile regression. An asymmetric Laplace distribution is assumed for the errors, so the regression models targets the specified quantile. A g-prior is assumed for the regression coefficients.

Usage

bqr(
  y,
  X,
  tau = 0.5,
  X_test = X,
  psi = length(y),
  nsave = 1000,
  nburn = 1000,
  nskip = 0,
  verbose = TRUE
)

Arguments

y

n x 1 vector of observed counts

X

n x p matrix of predictors

tau

the target quantile (between zero and one)

X_test

n_test x p matrix of predictors for test data; default is the observed covariates X

psi

prior variance (g-prior)

nsave

number of MCMC iterations to save

nburn

number of MCMC iterations to discard

nskip

number of MCMC iterations to skip between saving iterations, i.e., save every (nskip + 1)th draw

verbose

logical; if TRUE, print time remaining

Value

a list with the following elements:

  • coefficients the posterior mean of the regression coefficients

  • fitted.values the estimated tauth quantile at test points X_test

  • post_theta: nsave x p samples from the posterior distribution of the regression coefficients

  • post_ypred: nsave x n_test samples from the posterior predictive distribution at test points X_test

  • model: the model fit (here, bqr)

as well as the arguments passed

Note

The asymmetric Laplace distribution is advantageous because it links the regression model (X%*%theta) to a pre-specified quantile (tau). However, it is often a poor model for observed data, and the semiparametric version sbqr is recommended in general.

Examples

# Simulate some heteroskedastic data (no transformation):
dat = simulate_tlm(n = 100, p = 5, g_type = 'box-cox', heterosked = TRUE, lambda = 1)
y = dat$y; X = dat$X # training data
y_test = dat$y_test; X_test = dat$X_test # testing data

# Target this quantile:
tau = 0.05

# Fit the Bayesian quantile regression model:
fit = bqr(y = y, X = X, tau = tau, X_test = X_test)
#> [1] "0 seconds remaining"
#> [1] "Total time:  0 seconds"
names(fit) # what is returned
#>  [1] "coefficients"  "fitted.values" "post_theta"    "post_ypred"   
#>  [5] "model"         "y"             "X"             "X_test"       
#>  [9] "psi"           "tau"          

# Posterior predictive checks on testing data: empirical CDF
y0 = sort(unique(y_test))
plot(y0, y0, type='n', ylim = c(0,1),
     xlab='y', ylab='F_y', main = 'Posterior predictive ECDF')
temp = sapply(1:nrow(fit$post_ypred), function(s)
  lines(y0, ecdf(fit$post_ypred[s,])(y0), # ECDF of posterior predictive draws
        col='gray', type ='s'))
lines(y0, ecdf(y_test)(y0),  # ECDF of testing data
     col='black', type = 's', lwd = 3)


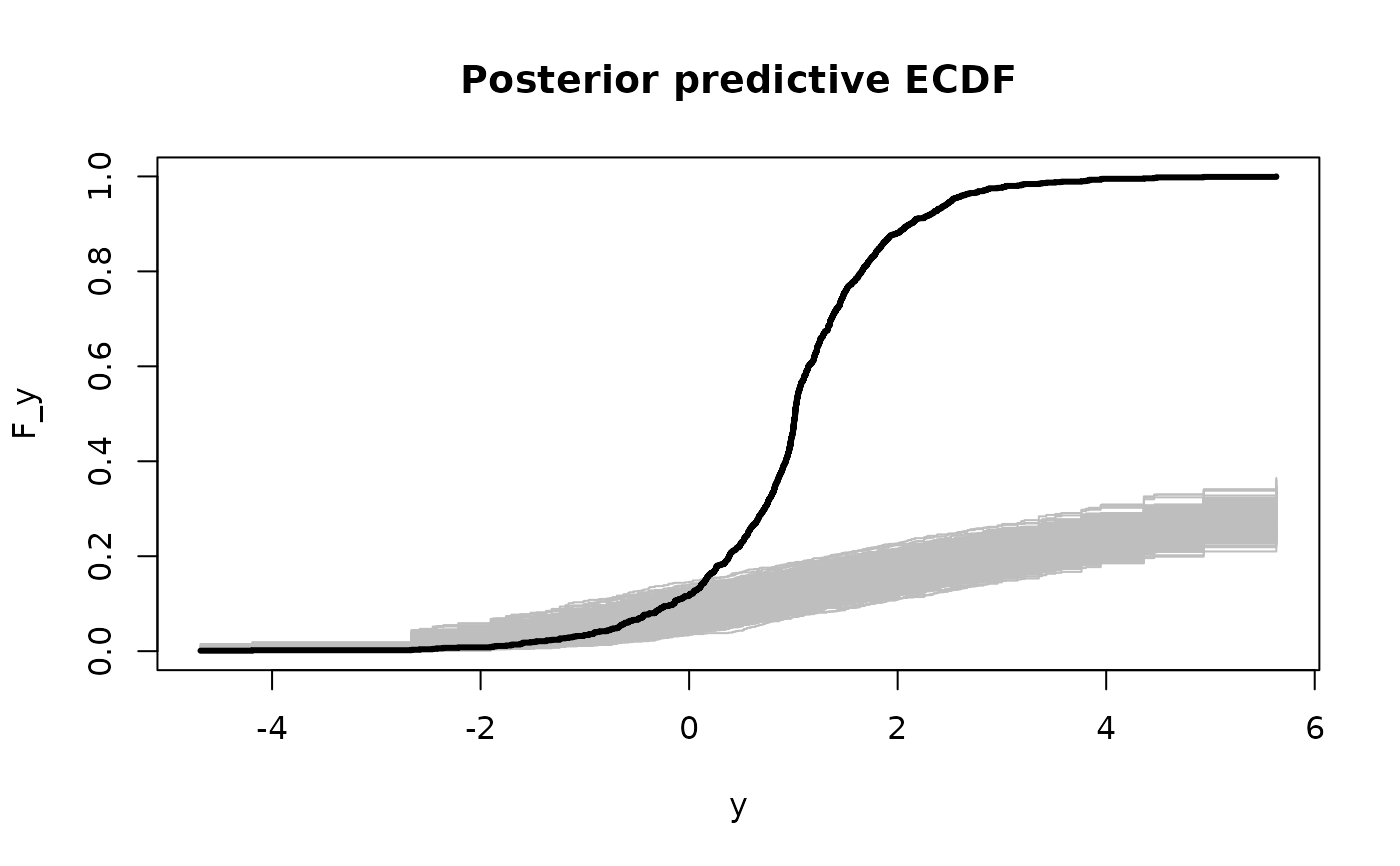# The posterior predictive checks usually do not pass!
# try ?sbqr instead...